Automated Market Making and Loss-Versus-Rebalancing

AMMs as sleepy price quoters in a high-frequency world

Jason Milionis, Ciamac Moallemi, Tim Roughgarden, and I just posted an update to our paper on Automated Market Making and Loss-Versus Rebalancing. Here’s the paper and abstract!

So what’s the paper about? To be a bit presumptuous, Loss-Versus-Rebalancing (LVR) aims to be essentially the Black-Scholes model for AMM liquidity provision. 

Black-Scholes serves two roles for studying option pricing. Qualitatively, BS shows how option returns depend on the underlying stock's return, volatility, and other parameters. Quantitatively, Black-Scholes is realistic enough to use for pricing options in practice.

LVR aims to play an analogous role for AMM liquidity provision. Qualitatively, LVR helps us understand the forces that make AMM LP losses bigger or smaller. Quantitatively, LVR is realistic enough to take to data: our formulas predict actual losses from LP-ing fairly well.

Black-Scholes begins by comparing options to replicating positions in the underlying stock. Similarly, our core idea is to compare AMM liquidity provision to a strategy which replicates the AMM's trades, but does so on a centralized exchange. Say you have an open USDC-wETH LP position; this position will trade USDC and wETH mechanically as prices move. Suppose you do exactly all the trades your LP position does, but you do them on Binance. We call this the "rebalancing strategy."

It turns out that, ignoring fees, your AMM LP position always does worse than the rebalancing strategy. Intuitively, this is because of price slippage: AMMs always trade at prices worse than CEX prices. Suppose you're LP-ing the USDC-wETH pair, and ETH prices on CEXes — say, Binance — increase a bit. Uniswap doesn't know prices have shifted: it only "realizes" this when it gets a bunch of buy orders. Your LP sells ETH, losing ETH inventory, until it eventually updates its price to the Binance price. Your LP loses money, since it could have made all these trades at the Binance price.

Here's a picture. Suppose ETH prices increase from Pt to Pt + dPt. The AMM trades from A to B, selling dxt ETH. But if we traded at price Pt + dPt, we could have gotten to B* instead! The vertical gap between B* and B is LVR. LVR also corresponds to arbitrageur profits from arbing Uniswap when Binance prices move: arbitrageurs can buy from the DEX at the A-B price, sell to Binance at the A-B* price, and make profit equal to the B* - B gap

Black-Scholes is used in practice to design trading strategies. Option market makers try to replicate options by "delta hedging" them using the underlying stock. This is essentially how MMs provide option liquidity in practice. Our theory similarly tells us that we can "delta-hedge" LP positions. This is very simple - you just short the rebalancing strategy, that is, you short as much ETH as your LP is long, at any point in time. A delta-hedged LP position eliminates "market risk" from ETH prices moving: it’s just a bet on whether you collect enough in fees to make up for what you lose in LVR price slippage.

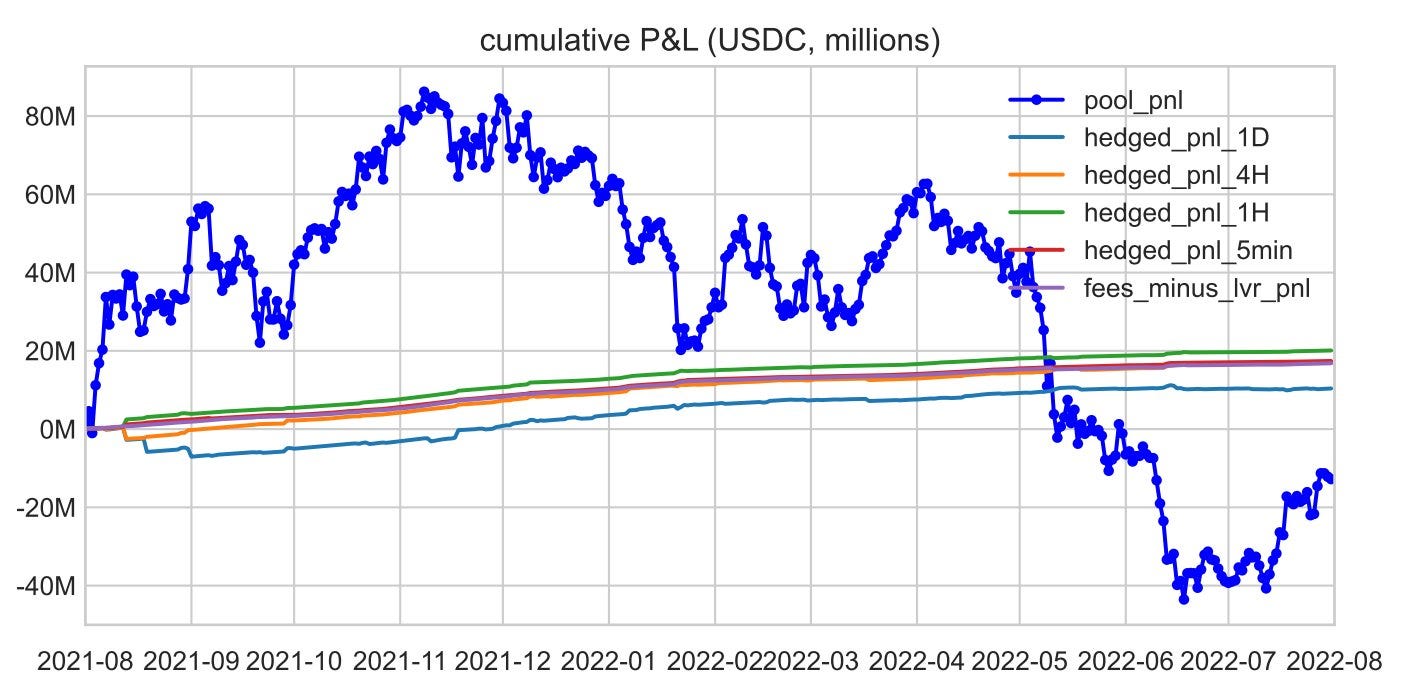
We then measure the returns from hedged and un-hedged LP-ing empirically for the Uniswap v2 WETH-USDC pair. We find that hedged LPing has a very different payoff profile from non-hedged LPing! The blue line shows raw unhedged LP P&L: it's super risky, basically because ETH prices move around a lot. But hedged LP-ing - the purple line -- is a very smooth, slightly increasing line.

If you're empirically studying the returns to AMM LP-ing, our "hedged LP-ing" approach could be a useful benchmark. You basically compare LP returns, to a strategy which does the same trades at market prices. See our Section 5 for details!

Our results matter for AMM design. AMM LPs lose money from price slippage: when Binance prices move, AMM quotes become “stale”. An obvious solution is that if AMMs updated price quotes when Binance prices move, LVR would be reduced. This is quite tricky to implement in practice — it requires a very high-frequency oracle, and is vulnerable to oracle manipulation attacks — but in theory with a perfectly fast and non-manipulable oracle, this could eliminate LVR.

Another possibility, which we first heard from Jump Crypto, is that AMMs could sell the right to arb the pool to CEXes to special wallets. Profits from these sales could then be redistributed to LPs. In principle, arbs should be willing to pay what their expected LVR (= arb profits) for arb rights, so this would also redistribute LVR to LPs in expectation. This is related to proposals to capture MEV by auctioning off tx ordering rights.

So that’s the paper. Let us know if you have any comments or questions!